——反步法实现反馈线性化控制器设计<1>
本文主要以一个例子粗浅的阐述反馈线性化如何作用于非线性控制系统并且使目标控制律以线性化后的反馈数据得出,撰写本文时,笔者尚未对非线性控制系统有完全和细致的了解,如有错漏万分抱歉。日后对非线性控制系统和反馈线性化更加了解后会进行勘误。特此感谢B站Up主Dr.CAN老师,他的视频对我的学习有非常大的帮助和意义,在此奉上Dr.CAN老师的主页链接。
本页内容概览
1.非线性系统例证理论推导
众所周知,控制系统(Control System)常常表征为一个微分方程,电气工程或者自动化专业学生在本科期间学习《自动控制原理》这门课程时常见的形式是如下展示的微分方程:
$$\sum\limits_{i=0}^{i\le n}{a_i\frac{d^{n-i}}{dt^{n-i}}c(t)}=\sum\limits_{j=0}^{j\le m}{b_j\frac{d^{m-j}}{dt^{m-j}}r(t)},\quad m\ge n$$
其中m通常大于等于n,这是因为如果作为输出函数的\(c(t)\)比$latext r(t)$的阶次要高则意味着系统中出现了理想微分器,很显然理想微分器是无法从物理上实现的,因为它在复频域中表现为\(\frac1s\)而在时域中表现为一个冲激偶函数\(\delta^{‘}(t)\),表征为一个非因果系统。我们经常使用的处理方式是将c(t)和r(t)同时进行Laplace变换从而实现从时域分析到复频域分析的过程。
当然在现代控制理论中,通常认为输入为一个时基函数\(u(t)\),输出为一个时基函数\(y(t)\),同时设定与系统阶次相同的n个状态变量时基函数\(x_i(t)\)组成状态向量\(x(t)=[x_1(t),x_2(t)\cdots x_n(t)]^T\)得到如下状态方程,ABCD为相应矩阵:
$$\begin{cases}\dot x(t)\,=\,\mathbf{A}x(t)\,+\,\mathbf{B}u(t) \\ y(t)\,=\,\mathbf{C}x(t)\,+\,\mathbf{D}u(t)\end{cases}$$
1.1非线性系统例证概述
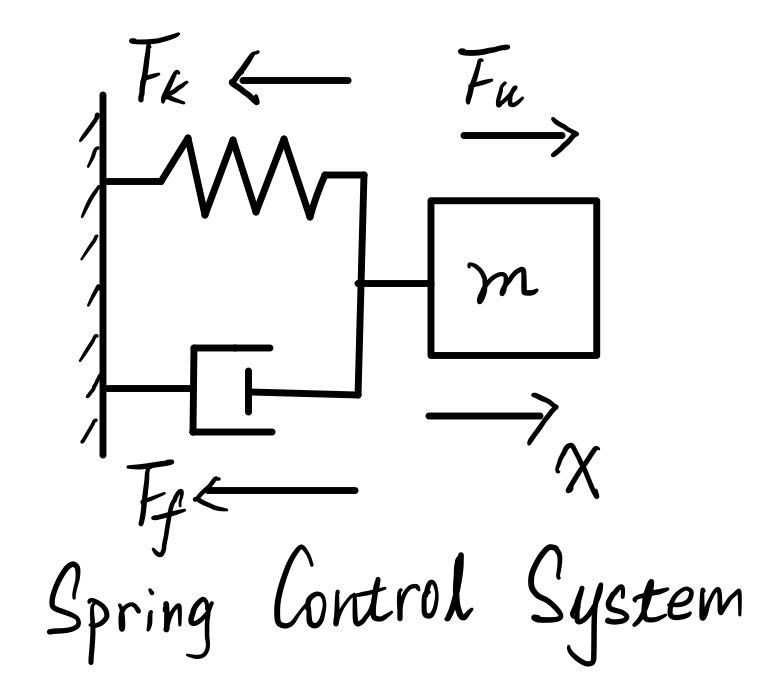
当系统中含有非线性项目时,传统的时域分析、频域分析、状态空间分析均无法使用,传统方法是通过相平面和描述函数分析后在系统某平衡点附近进行线性化展开并且讨论稳定性以及其他指标例如稳态误差\(E_{ss}\),但是我们寻求构造一种方法使该非线性控制系统通过线性化的反馈回路变换为一种状态空间的形式。现在考虑这样一种非线性控制系统如下图所示:
上图所展示的是一种非常常见的弹簧系统,传统系统下物块收到三个力:\(F_k\)代表因为弹簧形变收到的弹力\(F_k=\alpha x\),\(x\)代表质量为\(m\)的物块的正方向(右边)位移;\(F_f\)代表物块发生位移的过程中受到来自于缓冲活塞的阻力\(F_f=\beta v\),其中\(V\)代表着物块移动的正方向速度,同时\(F_u\)代表着正方向拉力的大小,这是系统的输入\(F_u=u(t)\)。在上图所示的非线性系统中,弹力和阻力发生了改变,我们假设这个系统中\(F_k=\alpha x^3, F_f=\beta \sin ^2v\)则可以得到如下所示的微分方程用于描述系统,其中\(\dot x\)代表速度,\(\ddot x\)代表加速度,均取向右的正方向:
$$System: \left\lbrace\begin{array}{c}F_u=u(t)\\F_k=\alpha x^3\\F_f=\beta\sin ^2\dot x\\m\ddot x=F_u-F_k-F_f\end{array}\right.\tag{1-1}$$经过整理得到:$$ m\ddot x=u-\alpha x^3-\sin ^2\dot x\tag{1-2}$$设定状态空间为\(x_1=x,\,x_2=\dot x\)则有状态空间形式:$$\left\lbrace\begin{array}{c}{\dot x=\begin {bmatrix}\dot{x_1}\\\dot{x_2}\end{bmatrix}=\begin{bmatrix}x_2\\-\frac{\alpha}{m}x_1^3-\frac{\beta}{m}\sin ^2{x_2}+\frac um\end{bmatrix}}\\y=x_1\end{array}\right.\tag{1-3}$$
1.2反步法构建一阶反馈
通过以上状态空间描述控制系统的形式,可以看到含有非常明显的非线性部分,反步法处理非线性系统的目标就是维持系统原有控制目标的状况下整理出线性化反馈构成的矩阵\(A\),在这个弹簧系统中控制目标即求一种控制率\(u(t)\)令系统输出\(y=x_d(t)\)其中\(x_d(t)\)为我们希望的物块位移。可以看到在系统中可以通过改变控制律\(u(t)\)来改变物块的速度和加速度,从而达到控制位移的目的,我们将这种形式的控制系统称之为Chain of Integrator,此类系统在生活中有很多,例如常见的无刷电机控制系统,汽车油门控制系统,空调调温系统。考虑\(x_{1d}(t)=x_d(t)\)则可以定义第一阶误差\(\epsilon\),显而易见控制目标为\(\epsilon\to 0\),作推导如下:
$$\epsilon=x_{1d}-x_1\tag{2-1}$$$$\dot\epsilon=\dot{x_{1d}}-\dot{x_1}\tag{2-2}$$将式1-3带入2-2可得:$$\dot\epsilon=\dot{x_{1d}}-x_2\tag{2-3}$$根据李雅普诺夫(Lyapnouv)稳定性理论,应当选取一个李氏函数\(V(\epsilon)\),令\(V(\epsilon)\gt 0\)且\(\dot V(\epsilon)\lt 0\)即函数本身正定但是一次导函数负定的控制律即可令系统稳定。因此选取李氏函数\(V_1(\epsilon)\)如下:$$V_1(\epsilon)=\frac 12\epsilon^2\tag{2-4}$$将式2-4代入可以求得\(\dot{V_1}(\epsilon)\)如下:$$\dot{V_1}(\epsilon)=\frac{\partial V_1}{\partial \epsilon}\times\frac{d\epsilon}{dt}=\epsilon\times (\dot {x_{1d}}-x_2)\tag{2-5}$$对于\((\epsilon,V_1(\epsilon))\)而言显然有点(0,0)既能够令系统误差为0也就是符合目标,又能够令李氏函数正定,考虑令$latex \dot{V_1}(\epsilon)负定,做如下设定:
$$\dot{x_{1d}}-x_2=-k_1\epsilon,\,k_1(\gt 0)\text{ is Controller Gain}\tag{2-6}$$$$\dot{V_1}(\epsilon)=-k_1\epsilon^2,\;when\,\epsilon\in\,\mathring{U}(0),\,\dot{V_1}(\epsilon)\text{ is ND}\tag{2-7}$$
1.3反步法构建二阶反馈
至此,第一层反步已经完成。可以看到在上一小节中完成了一阶反馈,将系统的控制目标明确为令一阶误差\(\epsilon\to 0\)即可达到系统的追踪也就是稳态误差为0,但是需要完成对于二阶系统的反馈线性化构建还需要构建第二层误差,仿照\(x_{1d}(t)\)的定义也可以定义\(x_{2d}(t)\)如下:$$x_{2d} =\dot{x_{1d}} +k_1 \epsilon\tag{3-1}$$显而易见,至此系统的控制目标已经发生了转移,当\(x_2 \to x_{2d}\)时系统稳定并且无稳态误差,引入第二阶误差\(\delta\)定义如下,求\(\delta\to 0\):
$$\delta=x_{2d}-x_2\tag{3-2}$$将式3-1与3-2代入式2-5得:$$\dot{V_1}=\epsilon[\dot{x_{1d}}-(x_{2d}-\delta)]=\epsilon(\dot{x_{1d}}-x_{2d})+\epsilon\delta=-k_1\epsilon^2+\epsilon\delta\tag{3-3}$$代入式1-3与式3-1可得到\(\dot\delta\)如下:$$\dot\delta=\dot{x_{2d}}-\dot{x_2}=\ddot{x_{1d}}+k_1\dot \epsilon-(-\frac{\alpha}{m}x_1^3-\frac{\beta}{m}\sin ^2{x_2}+\frac um)\tag{3-4}$$ $$\dot\delta=\dot{x_{2d}}-\dot{x_2}=\ddot{x_{1d}}+k_1(\dot{x_{1d}}-x_2)+\frac{\alpha}{m}x_1^3+\frac {\beta}{m}\sin ^2{x_2}-\frac um\tag{3-5}$$此时要求\(\delta\to0,\epsilon\to0\)并寻找一个新的李氏函数\(V_2(\epsilon,\delta)\)令函数本身正定,一次导函数负定达到系统稳定且无稳态误差:
$$V_2(\epsilon,\delta)=V_1+\frac12\delta^2=\frac12\epsilon^2+\frac12\delta^2,\,V_2\text{ is PD}\tag{3-6}$$代入式3-3与式3-6得出$$\dot{V_2}(\epsilon,\delta)=\dot{V_1}+\delta\dot\delta=-k_1\epsilon^2+ \epsilon\delta+\dot\delta\delta=-k_1\epsilon^2+\delta(\epsilon+\dot\delta)\tag{3-7}$$由前文分析得出,项\(-k_1\epsilon^2\)必然负定,则要求项\(\delta(\epsilon+\dot\delta)\)负定,因此做如下设定:$$when\,\epsilon+\dot\delta=-k_2\delta,\,\delta(\epsilon+\dot\delta)=-k_2\delta^2\text{ is ND}\tag{3-8}$$类似于\(k_1\)的定义,\(k_2\gt 0\)也是一个控制器增益系数,根据式3-8的定义\(V_2\) 是负定的,此时展开3-8式中对于\(k_2\)的定义代入式3-5,可以得到下式:
$$\epsilon+\ddot{x_{1d}}+k_1(\dot{x_{1d}}-x_2)+\frac{\alpha}{m}x_1^3+\frac {\beta}{m}\sin ^2{x_2}-\frac um=-k_2\delta\tag{3-9}$$整理得到控制律\(u(t)\)如下,至此第二阶反步完成,对于二阶非线性系统,即求得使系统稳定且能够跟随目标状态的控制律:$$u=\alpha x_1^3+\beta\sin ^2x_2+m\epsilon+m \ddot{x_{1d}}+mk_1(\dot{x_{1d}}-x_2)+mk_2\delta\tag{3-10}$$
1.4根据控制律结果验证反馈线性化构建结果
在上一小节中完成了控制律推。现在根据控制律的推导进行验证,目标是推导出两个误差变量构成的误差向量的导数与误差向量的关系,并且根据系数矩阵进行李雅普诺夫分析以证明反步法进行反馈线性化的稳定性和追踪性能。现在开始分析,首先将式3-2代入式2-3得到下式:
$$\dot\epsilon=\dot{x_{1d}}-(x_{2d}-\delta)\tag{4-1}$$将式3-1代入上式得:$$\dot\epsilon=-k_1\epsilon +\delta\tag{4-2}$$将式3-10的控制律代入式3-5验证\(\dot\delta\)如下:$$\dot\delta=-\epsilon-k_2 \delta\tag{4-3}$$综合式4-2与式4-3得到线性化后的误差式如下,即完成反馈线性化:$$\begin{bmatrix}\dot\epsilon\\\dot\delta\end{bmatrix}=\begin{bmatrix}-k_1&1\\-1&-k_2\end{bmatrix} \begin{bmatrix}\epsilon\\\delta\end{bmatrix},\,\Lambda=\begin{bmatrix}-k_1&1\\-1&-k_2\end{bmatrix} \tag{4-4}$$对矩阵\(\Lambda\)进行分析,设该矩阵的两个特征值为\(\lambda_1,\lambda_2\)根据基础的线性代数分析可以得出:$$ \begin{cases}\lambda_1+\lambda_2=tr(\Lambda)=-k_1-k_2\lt 0\\ \lambda_1\times\lambda_2=det(\Lambda)=k_1\times k_2+1\gt 0\end{cases}\tag{4-5}$$由上述分析可以得出\(\lambda_1\lt 0,\lambda_2\lt 0\)那么在平衡点\((\dot\epsilon,\dot\delta)=(0,0)\Rightarrow (\epsilon,\delta)=(0,0)\)时又因为特征值全部为负数,由李氏判据得出系统在此平衡点渐进稳定(Asympototically Stable)。至此得出结论,反馈线性化(FeedBack Linearization)完成。
2.使用Simulink完成例证分析
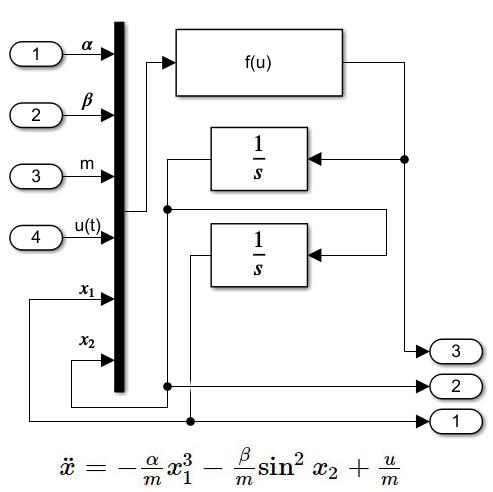
如下图所示封装非线性弹簧系统本身,该子系统具有四个外部输入分别为三个系数\(\alpha,\beta,m\) 代表弹簧系统的弹力系数、阻力系数以及滑块质量,第四个输入为施加的外部拉力\(F=u(t)\)。图中的f(u)模块是System Function模块,他的作用是根据输入的六个参数计算出\(\ddot x\),该函数的第五个和第六个参数分别是\(x_1=x,x_2=\dot x\),由输出进行两次和一次积分取得。子系统拥有三个输出,分别是\(x,\dot x,\ddot x\)用于观测系统状态和后续完成反馈线性化使用。
2.1 Simulink验证反步法的合理性与典型信号响应
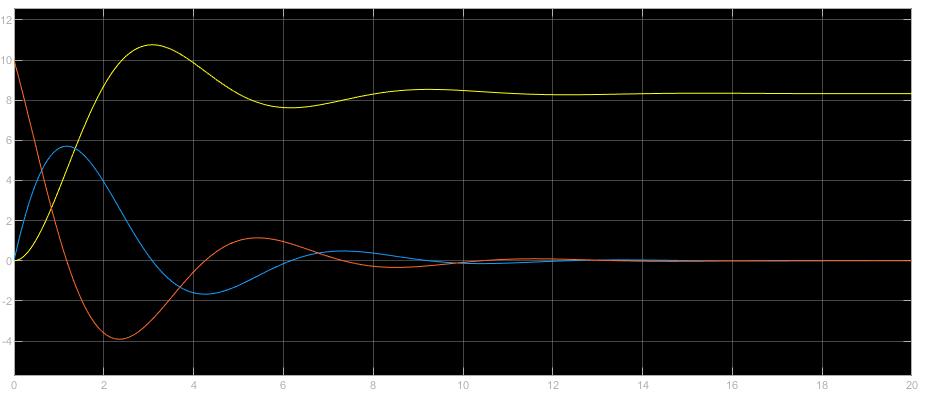
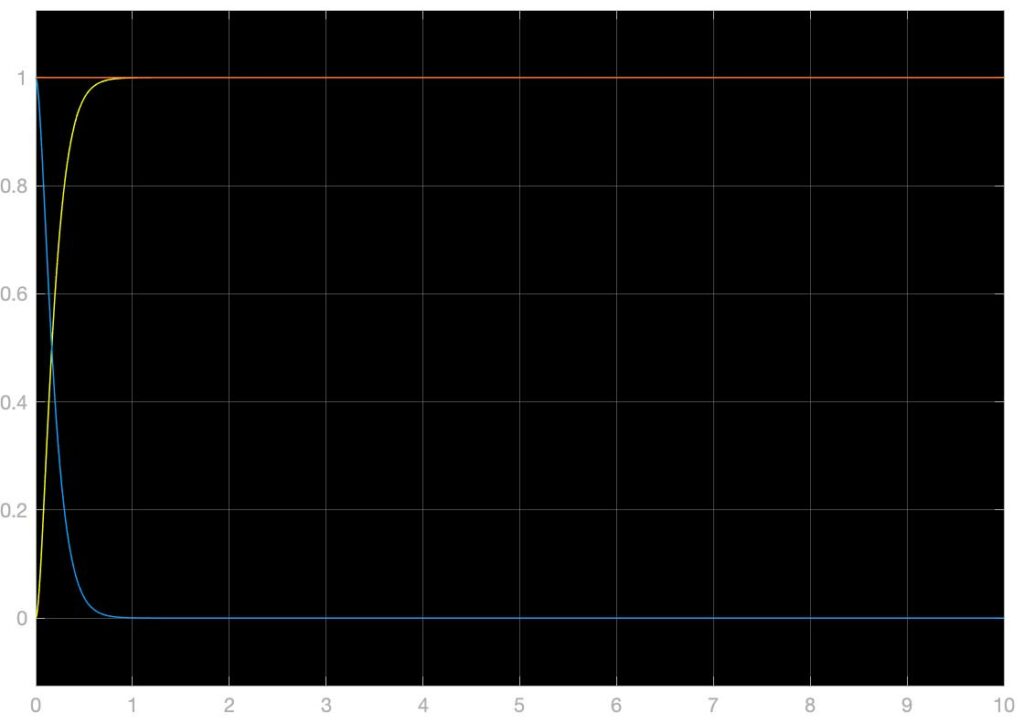
改变系统函数为\(f(u):\ddot x=-\frac\alpha mx_1-\frac\beta mx_2+\frac um\)即可将非线性弹簧系统复原为线性二阶弹簧系统,设定参数为\(\alpha=1.2,\beta=0.8,m=1,u(t)=step(t=0,10)\)得到典型二级系统欠阻尼相应如下,其中黄色为位移,蓝色为速度,红色为加速度:
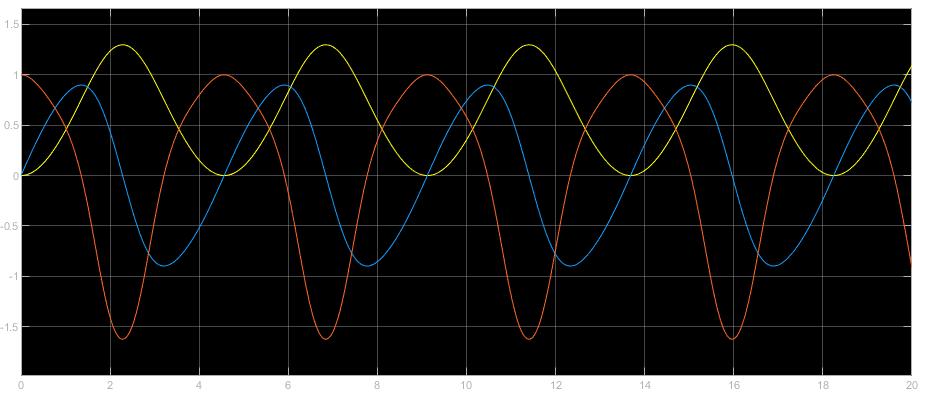
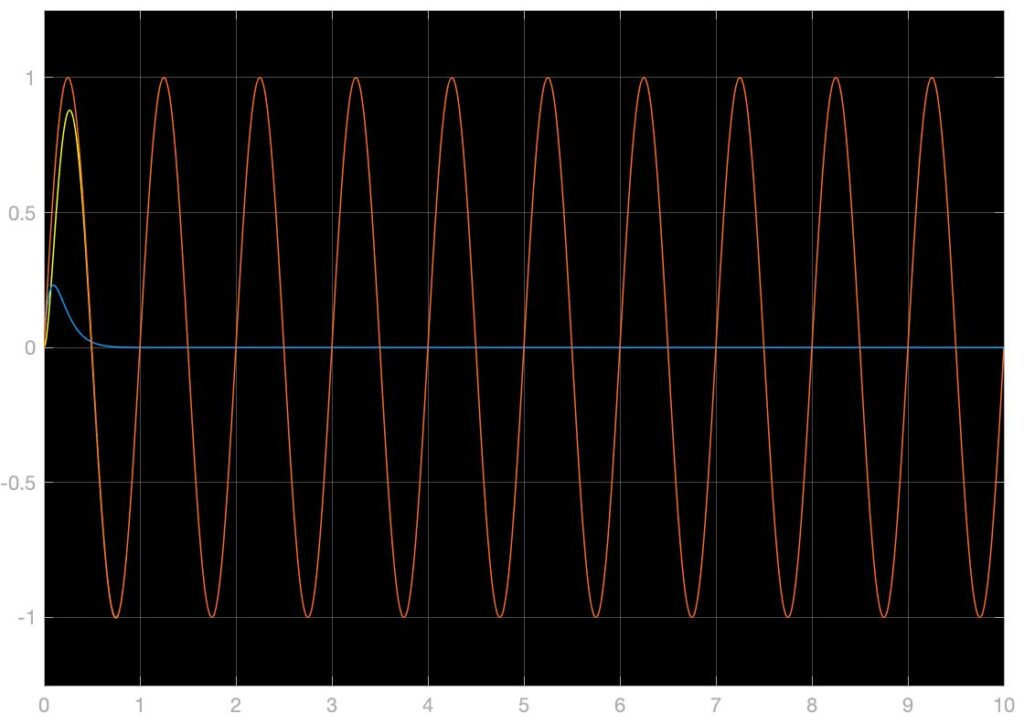
将同样的参数配置输入到非线性弹簧系统中得到的单位阶跃响应如下所示,可以看到,非线性环节大大的影响了系统的响应并且使之畸变,产生了一定程度的自激振荡:
根据上文分析,构建Simulink反步法非线性系统控制,如下图所示,整个系统由五个部分构成,第一部分是上文展示的非线性弹簧模拟模块,第二部分是使用反步法思想实现两个误差\(\epsilon,\delta\)的计算推导,第三部分是通过周期性阶跃信号(此周期应大于系统进入稳态的时间)与正弦震荡信号的组合实现目标信号以及其导函数的实现,第四部分是可变参数的设定,第五部分是综合相关12个参数计算得出理论上能够实现控制目标的输入信号控制律;最后设定对于\(x,x_{1d},\epsilon,\dot x,\ddot x,u\)的观测用示波器查看系统性能,模拟整体框图如下:
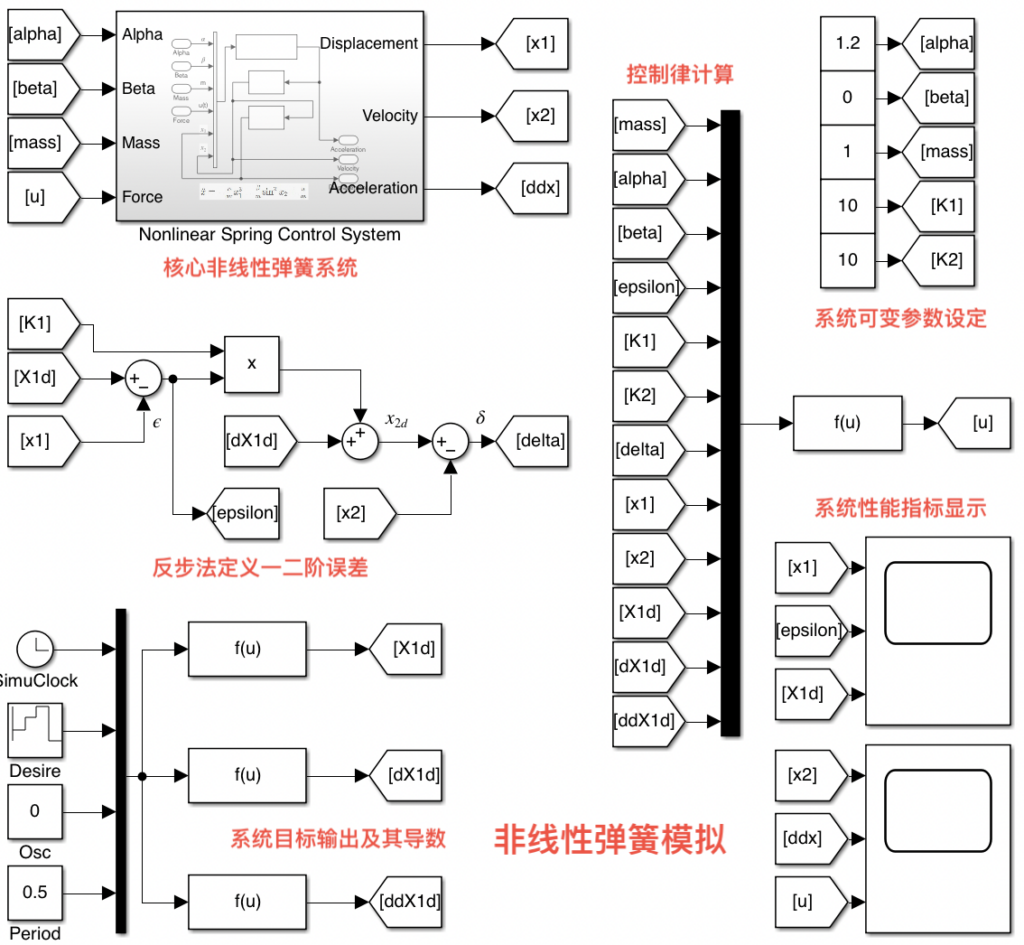
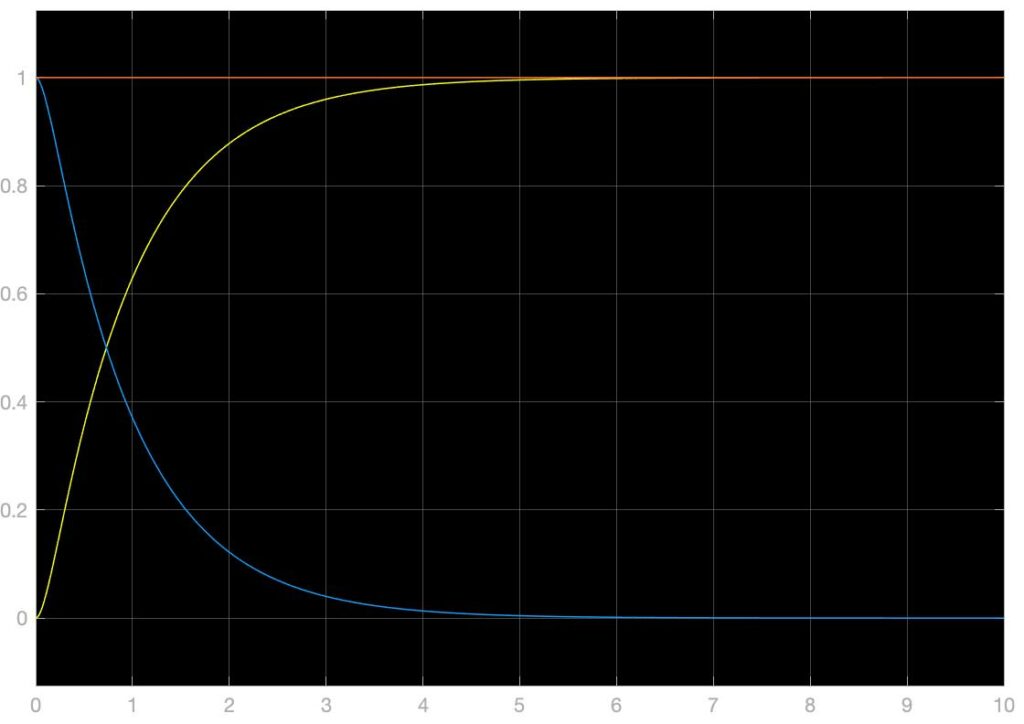
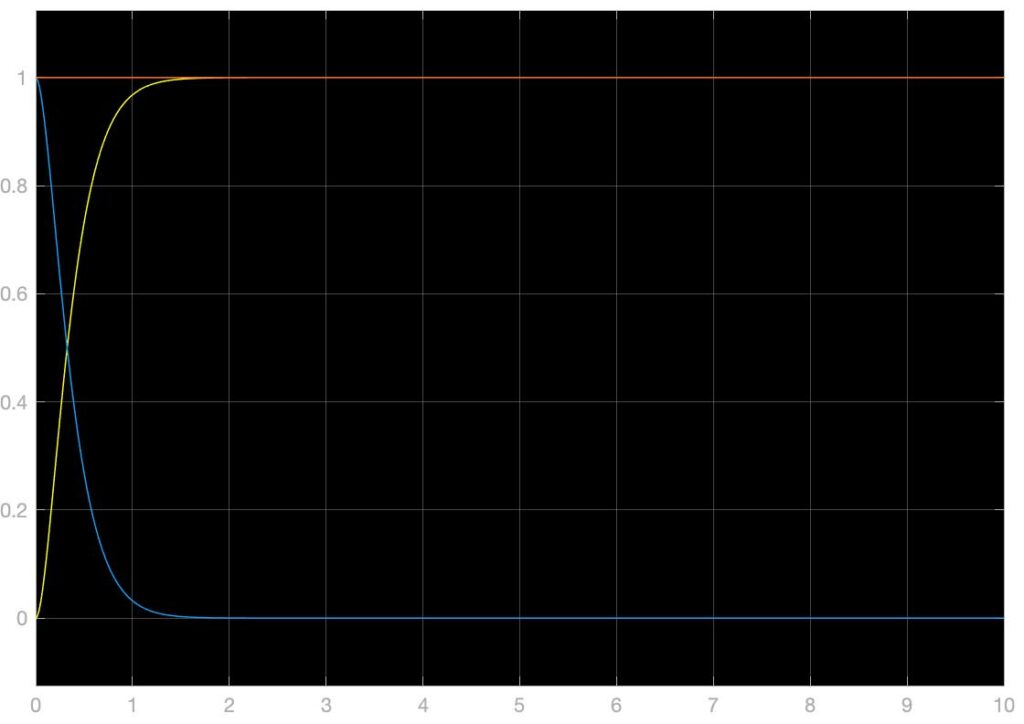
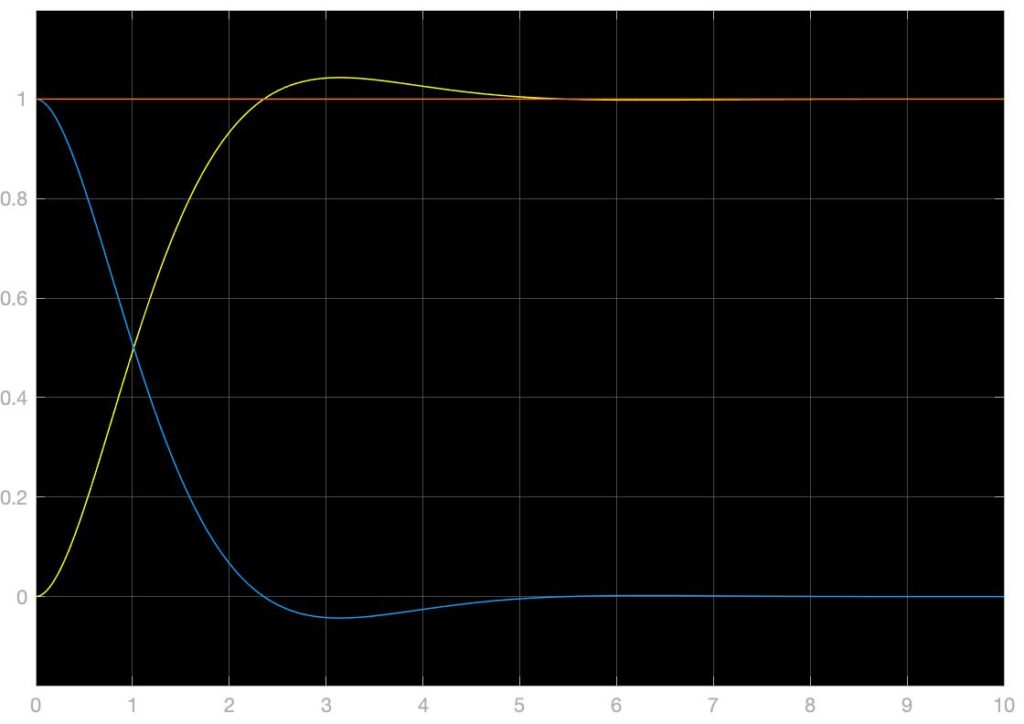
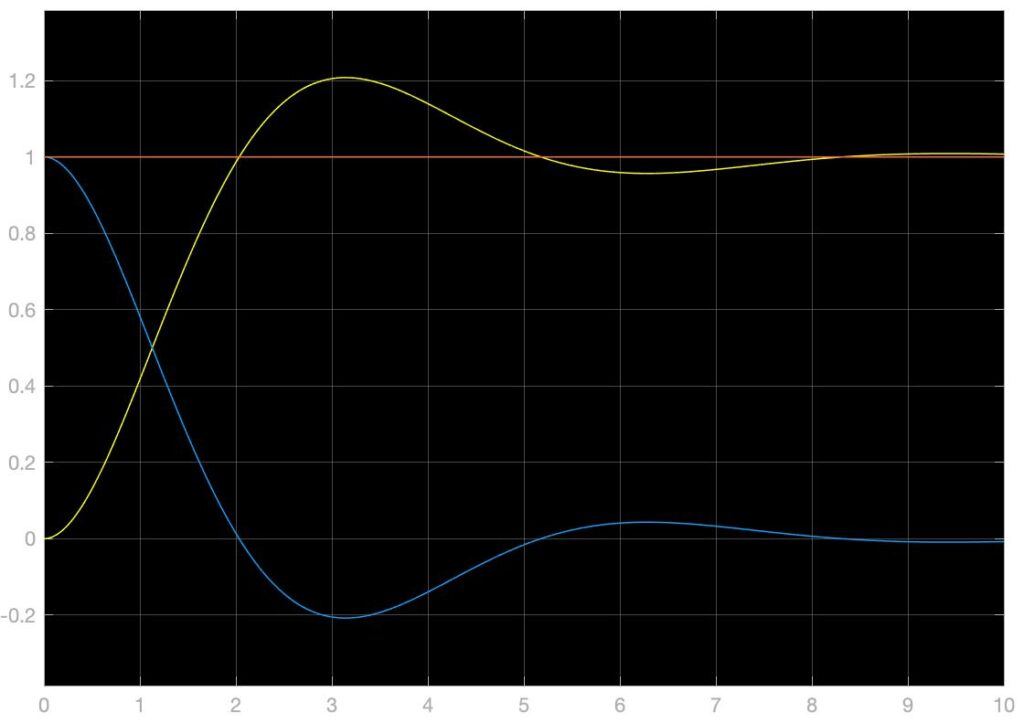
上图中所展示的模拟系统中,Osc代表目标输出信号及其导函数中正弦震荡信号的振幅,Desire代表着一个周期性重复的阶跃信号组,Period代表着正弦信号的周期,单位为秒。\(k_1,k_2\)为反步法构建线性化反馈控制器的增益,改动这两个值可以改动系统的特征值和特征向量,改变系统的响应效果。在上图展示的系统和参数的状况下,单位阶跃响应,单位正弦信号响应,以及混合信号响应如下,黄色为系统输出,蓝色为实时误差,橙色为目标输出信号:
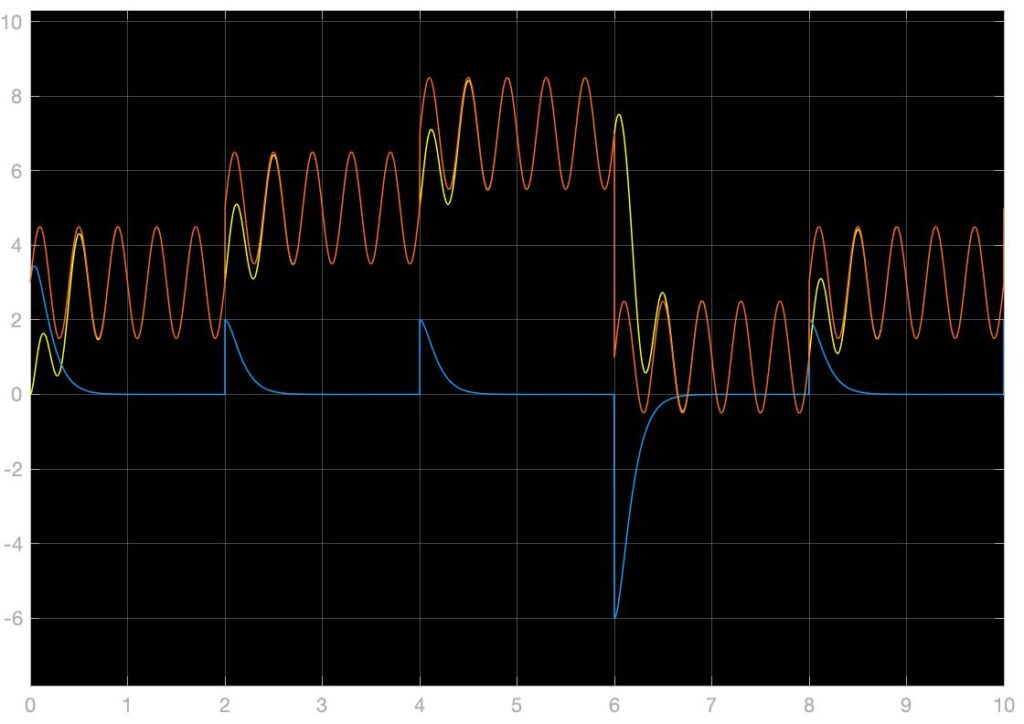
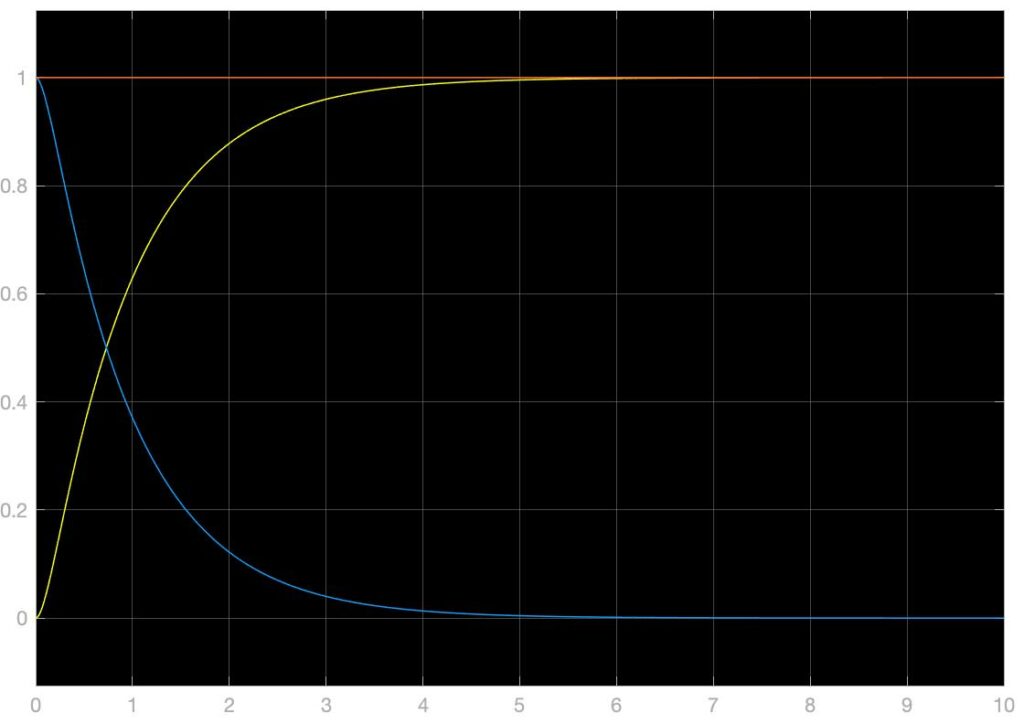
以上仿真结果主要展示了\(k_1=10,k_2=10\)的参数情况下完成的,可以看到,此时的单位阶跃响应输出结果中,没有稳态误差,稳态时间约为0.8s。下面展示$k_1,k_2$分别为(1,10)、(10,1)、(5,5)、(1,1)、(0.5,0.5)时系统的单位阶跃响应,可以发现\(k_1\bullet k_2\)越大系统的响应速度就越快,而此两个参数对称分布乘积不变时,似乎没有大的影响:
2.3 对比反馈线性化控制器与PID控制器效果
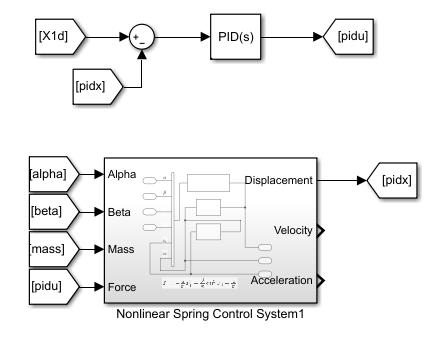
具体关于反步法设计反馈线性化控制器的参数整定、控制器增益带来的影响的分析、反步法的缺陷与优势以及改进方法将在以后的文章中进一步阐述,为了直观的简单的与传统控制方案进行对比,构建如下图所示的PID控制器:
下面列出传统PID控制器与反步法控制器的单位阶跃响应的对比图,黄色曲线为反步法控制器响应,蓝色曲线为传统PID控制器响应,橙红色曲线为系统目标输出。可以看到在左图中,假设主动力\(F_u\)使用一个电机+减速箱提供,在同等扭力的冲击下:PID控制器超调量较大,而反步法控制器表现出过阻尼的性质;PID控制器调节时间和上升时间较长,反步法控制器的调节相应速度明显较为迅速。在右图中展示的是仅仅要求两个控制器稳态时间相同的状况下,PID控制器下的电机扭力需求度大大高于反步法控制器,这在实际的控制过程中对于伺服系统的动力是毁灭性的打击。


3. 对更加有普遍性的系统使用反步法
上文已经讨论了对于一个二阶非线性弹簧系统的反步法控制器设计,现在将对于N阶非线性系统,两个及以上状态变量耦合的状况,不确定扰动与系统耦合,对非线性扰动添加非线性阻尼的种种情况进行讨论,试图找出一种普遍化的,流程化的反步法建立控制器求解控制律的方法。
3.1 对N阶非线性系统的简单反步法控制器设计
现考虑一个n阶非线性系统的状态空间表示如下,显然系统的状态空间变量的建立方式遵循上文提到的积分式(Chain of Integrator)故有通式\(\dot x_i=x_{i+1}+\Delta f_i(x_i),i\in[1,n-1]\),在通式中可以看到一个非线性函数项\(\Delta f_i(x_i)\)代表在状态空间的建立过程中每个变量的“非线性误差”,显然在前文的例子中这个非线性项为0,系统整体如下:
$$\left\lbrace\begin{array}{c}\dot x_1=x_2+\Delta f_1(x_1)\\ \dot x_2=x_3+\Delta f_2(x_2)\\ \cdots\\ \dot x_n=f(x_1)+g(x_1)u+\Delta f_n(x_n)\end{array}\right.\tag{5-1}$$可以看到对于最后一个状态变量\(\dot x_n\)有一个特殊的处理,式子由非线性项、关于\(x_1\)的函数\(f(x_1)\)与输入项u和函数\(g(x_1)\)的乘积构成,反步法进行到这里将求出控制律,先来做第一步,第一层的目标输出即为整个系统的目标输出:
$$\text{define error: }\epsilon_1=x_{1d}-x_1\tag{5-2}$$经过对于第一层误差的定义,系统的控制目标转移为\(\epsilon_1\to0\)并且选定Lyapunov函数\(V_1(\epsilon)=\frac 12\epsilon_1^2\)显然这个函数本身是正定的,要求其导函数负定,推导如下:$$\dot V_1(\epsilon)=\frac{\partial V}{\partial \epsilon_1}\times \frac {d\epsilon_1}{dt}=\epsilon_1(\dot x_{1d}-\dot x_1)\tag{5-3}$$如果要求\(\dot V_1(\epsilon)\)负定以达到李氏稳定中的渐进稳定则做如下推导:$$\text{if }(\dot x_{1d}-\dot x_1)\to-k_1\epsilon_1\text{ then }\dot V_1 (\epsilon)\text{ is ND}\tag{5-4}$$其中\(k_1\gt0\)是一个控制器增益系数,可以得出对\(x_2,\,x_{2d}\)的推导如下:
$$\dot x_{1d}-[x_2+\Delta f_1(x_1)]\to -k_1\epsilon_1\tag{5-5}$$
$$x_2\to \dot x_{1d}+k_1\epsilon_1-\Delta f_1(x_1)\tag{5-6}$$由上式定义\(x_{2d},\,\epsilon_2\)并将控制系统的条件转移为\(\epsilon_2\to0\),推导如下:$$x_{2d}=\dot x_{1d}+k_1\epsilon_1-\Delta f_1(x_1)\tag{5-7}$$ $$\epsilon_2=x_{2d}-x_2\tag{5-8}$$ $$\dot V_1(\epsilon)=\epsilon[\dot x_{1d}-(x_{2d}-\epsilon_2-\Delta f_1)]\tag{5-9}$$ $$\dot V_1(\epsilon)=\epsilon_1(\dot x_{1d}-x_{2d}+\Delta f_1)+\epsilon_1\epsilon_2=-k_1\epsilon_1^2+ \epsilon_1\epsilon_2\tag{5-10}$$结合第一层反步的推导和上文的推导可以得到\(i\in[2,n]\)情况的通式如下:
$$x_{id}=\dot x_{(i-1)d}+k_{i-1}\epsilon_{i-1}-\Delta f_{i-1}(x_{i-1})+\epsilon_{i-2}\tag{6-1}$$上式中\(\epsilon_0=\epsilon_{-1}=0\),根据\(x_{id}\)的推导,可以得到在条件\(i\in[1,n-1]\)下的\(V_i(\epsilon)\)如下:$$V_i(\epsilon)=\sum_\limits{j=1}^{j\le i}(\frac 12 \epsilon_j^2)\tag{6-2}$$ $$\dot V_i(\epsilon_1\cdots \epsilon_i)=\sum_\limits{j=1}^{j\le i}\dot V_j(\epsilon)= \sum_\limits{j=1}^{j\le i}-k_j\epsilon_j^2+\epsilon_i\epsilon_{i+1}\tag{6-3}$$完成前n-1阶反步法的李氏函数推导与前n阶的目标输出的推导后,对n阶反步法处理得到控制律:$$\dot V_n(\epsilon_1\cdots \epsilon_n)=\sum_\limits{i=1}^{i\lt n-1}-k_i\epsilon_i^2+\epsilon_n(\epsilon_{n-1}+\dot\epsilon_n)\tag{6-4}$$可以看到如果要求\(\dot V_n(\epsilon_1\cdots\epsilon_n)\)负定,则要求\(\epsilon_{n-1}+\dot\epsilon_n\to-k_n\epsilon_n\)则有如下等式:
$$\epsilon_{n-1}+(\dot x_{nd}-\dot x_n)=-k_n\epsilon_n\tag{6-5}$$ $$\epsilon_{n-1}+[\dot x_{nd}-f(x_1)-g(x_1)u -\Delta f_n(x_n)]=-k_n\epsilon_n\tag{6-6}$$ $$u=\frac 1{g(x_1)}[\epsilon_{n-1}+\dot x_{nd}-f(x_1)-\Delta f_n(x_n) +k_n\epsilon_n]\tag{6-7}$$上式即为所求控制律u的表达式,代入上文中非线性弹簧系统的相关参数,得到与式3-10完全一致的控制律表达式。现对各阶误差进行分析,首先分析前n-1阶:
$$\dot\epsilon_i=\dot x_{id}-\dot x_i=\dot x_{id}-[x_{(i+1)d}-\epsilon_{i+1}+\Delta f_i(x_i)]\tag{6-8}$$
$$\dot\epsilon_i=-k_i\epsilon_i+\epsilon_{i+1}-\epsilon_{i-2},\,i\in[1,n-1]\tag{6-9}$$对于\(\epsilon_n\)有如下分析并代入上文求出的控制律u的表达式:$$\dot \epsilon_n=\dot x_{nd}-\dot x_n=\dot x_{nd}-[f(x_1)+g(x_1)u +\Delta f_n(x_n)]\tag{6-10}$$ $$\dot \epsilon_n=-k_n\epsilon_n-\epsilon_{n-1}\tag{6-11}$$如此可以得到n阶误差构建的反馈线性化矩阵如下:
$$\begin{bmatrix}\dot\epsilon_1&\dot\epsilon_2&\cdots&\dot\epsilon_{n-1}&\dot\epsilon_n\end{bmatrix}^T=\mathbb{\Lambda}\begin{bmatrix}\epsilon_1&\epsilon_2&\cdots&\epsilon_{n-1}&\epsilon_n\end{bmatrix}^T\tag{6-12}$$
$$\mathbb{\Lambda}=\begin{bmatrix}-k_1&1&0&0&\cdots&0&0&0&0\\0&-k_2&1&0&\cdots&0&0&0&0\\-1&0&-k_3&1&\cdots&0&0&0&0\\0&-1&0&-k_4&\cdots&0&0&0&0\\\vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots&\vdots\\0&0&0&0&\cdots&-k_{n-3}&1&0&0\\0&0&0&0&\cdots&0&-k_{n-2}&1&0\\0&0&0&0&\cdots&-1&0&-k_{n-1}&1\\0&0&0&0&\cdots&0&0&-1&-k_n\end{bmatrix}$$设该矩阵的n个特征值为\(\lambda_1, \lambda_2,\cdots,\lambda_n\)且设该n阶方阵为\(\Lambda\),则有如下分析:
$$\begin{cases}\lambda_1\times\lambda_2\times\cdots\times\lambda_n=det(\Lambda)\lt0,\text{n is odd; }\gt0,\text{n is even}\\\lambda_1+\lambda_2+\cdots+\lambda_n=tr (\Lambda)=-k_1-k _2-\cdots-k_n\lt 0\end{cases}\tag{6-13}$$可以看到所有特征值的和也就是矩阵的迹一定是负数,而所有特征值的乘积,也就是矩阵的行列式值完全可能支持所有特征值都是负数这一可能性,故而这种反步法构建的控制器一定能够找到使系统稳定的k的解,当然有可能是多个解。
PS:参考材料列表
CSDN:全网最细反步法控制(Backstepping)simulink设计与实例讲解!!(1) CSDN:反步(Back-Stepping)设计方法 知乎:(五)反步控制零基础讲解——作者:硬核暴龙 B站:【Advanced控制理论】15_Nonlinear Backstepping Control_反馈线性化控制