拉格朗日力学(Lagrange)与分析方法基础

——Lagrange分析方法

不同于高中物理和大学基础物理中的描述，牛顿力学只是经典力学的中的一部分，牛顿力学主要是以相对性原理和伽利略变换为框架，提出牛顿相对定律和矢量分析的力学。经典力学中还包括两个主要部分，分别是拉格朗日力学和哈密顿力学，不同于牛顿力学着眼于矢量分析（因此被称为矢量力学）的分析方式，拉格朗日力学主要着眼于系统的能量等指标，通过变分原理建立系统动力学方程，所以拉格朗日和哈密顿的力学可以称之为分析力学。

1.牛顿力学的局限性——以单摆为例子

在牛顿力学中，主要还是通过牛顿运动定律确定物体的运动状态，首先使用牛顿第二定律建立方程\(\vec F(\vec r)=m\ddot {\vec r}\)，其中力的矢量一般可以通过力学分析得到，结合微分方程的初始条件可以得到物体的运动方程\(\vec r=\vec r(t)\)，可以结合笛卡尔直角坐标系得到更加精确和直观的矢量分析结果即\(\vec r=x\vec r_x+y\vec r_y+z\vec r_z\)，则有如下经典形式：

$$\begin{cases}x=x(t)\\y=y(t)\\z=z(t)\end{cases},\,\begin{cases}F_x=m\ddot x\\F_y=m\ddot y\\F_z=m\ddot z\end{cases}\tag{1-1}$$

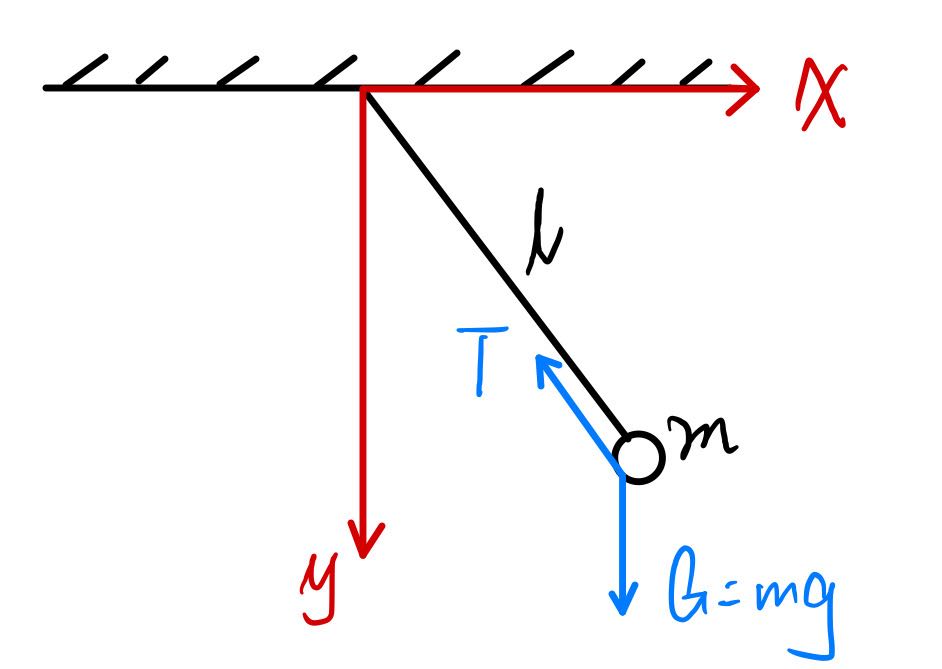
这种经典分析在遇上非惯性系或者说非线性系统的时候会展现出极大的局限性，此刻作为例子考虑一个经典问题：单摆的运动，这个二维问题如下所示，小球显然收到两个力，一个是重力G一个是重力T，摆杆或者说摆绳长度为l，建立坐标系并可以得到1-1式方程在本问题中的展开：

$$\left\lbrace\begin{array}{c}-T\frac{x}{\sqrt{x^2+y^2}}=m\ddot x\\mg-T\frac{y}{\sqrt{x^2+y^2}}=m\ddot y\end{array}\right .\tag{1-2}$$根据朴素的基础数学知识，可以发现这个方程组由两个方程构成但是未知数显然有三个量T，x，y所以这个方程理论上来说是解不出来的。当然根据常识这种“简单模型”是易于求解的所以说在建模过程中一定是漏掉了一些约束条件才导致了模型的缺损。可以发现，物体的运动收到了摆绳的约束，也就是拉力的约束，这种力可以称之为约束力，当然模型中的几何关系也对于小球的运动构成了数学上的约束，称之为几何约束，我们将如下约束补全到模型中去：$$x^2+y^2=l^2\tag{1-3}$$但是问题是这个方程非常难以求解，即使是使用Laplace变换这种手段也存在局限性：带入约束条件后1-2中的两个方程耦合了起来，也就是说x和y方向上的独立性被破坏了。

现在考虑使用广义坐标消去约束力，在描述单摆运动方程中，使用的是笛卡尔坐标系中的x和y两个分量去描述小球的运动状态，而不幸的是在这个例子中由于几何约束这两个变量耦合了。这两个变量的非独立性界定了不需要用两个变量单独表述运动状态，只需要选择其中一个变量即可，一种非常自然的想法是将摆绳与法线之间的夹角\(\theta\)作为新的描述系统运动的唯一变量得到如下方程：

$$ \left\lbrace\begin{array}{c}T-mg\cos\theta=0\\mg\sin\theta-ml\ddot\theta=0\end{array}\right .\tag{1-4}$$如果考虑较小角度运动时\(\theta=\sin\theta\)那么这个方程就更加容易求解了。此处使用了极坐标进行求解，但是它属于一个更大的类别：广义坐标。

广义坐标并不依赖于某个坐标系而建立，它甚至能够无视平动和转动的区别，是一种不特定的坐标，只要它能够表述力学系统和运动系统的状态即可，合理推论，对于有约束力的问题，只要变笛卡尔直角坐标系为某种契合约束方式的广义坐标系就可以解决大多数问题，比较常见的广义坐标系例如在高等数学教科书中出场频率较高的柱坐标系和球坐标系。

在更复杂的动力学问题中要消去约束力可能要面临一个约束力的重要性质：约束力不做功，例如在上述问题中明显约束力T和运动方向呈现出直角，因此完全不做功；又比如一个可以看作质点的光滑刚体小球在某个光滑曲面上做工的时候，曲面给予小球的支持力顺应曲面的法向方向，因此不做功。要完整并且严谨的表述这一性质需要引入一个新的概念：虚位移。在高中物理和基础大学物理中，一般认识的位移称之为实位移，也就是真实存在的位移，是有其物理实现的；而虚位移一般指的是虚拟的假想的一种位移，这种位移很多时候是只存在于逻辑推导之中的，很可能无法直接找到其物理实现。虚位移可以较为严谨的定义：在时间和空间位置确定的状况下，虚位移是符合约束条件的任意无穷小位移。符号:\(\delta\vec r\)同样虚位移也有和实位移定义相同的虚功等概念，虚功即力和虚位移的内积，也是一个标量。

考虑一个简单的例子，就是上文中提到的刚体小球在光滑表面运动的例子，约束力显然是支持力，由于这个力永远与运动方向垂直，所以约束力的虚功为0；但是如果考虑有两个完全一样的刚体小球在这个光滑表面运动，区别是他们之间使用一根没有质量的刚体杆连接，那么对于其中一个小球而言，杆体对小球的作用力也是约束力，但是虚功显然不为0，这时候就要讨论：多质点系统中，考虑约束力对于整个系统的虚功这一问题。虚位移在此系统中受到的约束可以表示为如下式子，r代表位移而l代表杆长：

$$(\vec r_1-\vec r_2)^2=\ell^2\tag{1-5}$$因为虚位移的定义是一个无穷小的位移，所以需要对上式进行一次微分运算，推导如下：$$d(\vec r_1-\vec r_2)^2=d(\ell^2)\tag{1-6}$$ $$2(\vec r_1-\vec r_2)(d\vec r_1-d\vec r_2)=0\tag{1-7}$$由于$\latex \delta$运算与微分运算规则基本相同，在这个例子中可以相互替换使用，当然他们之间的数学物理意义还是有区别的。通过牛顿第三定律，刚性连杆对于两个小球的作用力是等大反向的，并且和两个小球的连线是共线的，设两个作用力为\(\vec N_1,\vec N_2\)则有如下定义与推导：

$$\vec N_1=-\vec N_2=\lambda(\vec r_1-\vec r_2),\lambda \neq 0\text{ is a constant}\tag{1-8}$$将上式代入式1-7中可得虚功表达式：$$\delta W=\vec N_1\delta\vec r_1+\vec N_2\delta\vec r_2=\lambda(\vec r_1-\vec r_2)(\delta \vec r_1-\delta \vec r_2)\tag{1-9}$$由约束条件可得虚功为0，故而可以得到在此系统中：力学系统所受到的约束力的总虚功为0。 注意，这条结论的推导状况需要满足理想约束，也就是一般系统中的“光滑无摩擦”，此处的定义可能并不严谨，但是并不影响对于这种力学系统的理解。

2.拉格朗日方程推导

在上文中通过简单的证明与思考得到了如下结论：力学系统中所受到的理想约束力做的总虚功为零。如果要从系统的能量和各个质点的做功出发考虑力学系统，那么就需要消掉理想约束的虚功，也就需要借助于达朗贝尔定理，这是一个相对简单的力学定理，也非常符合直觉故而不做过多说明与证明，关于其详细内容可以参见百度文库词条。使用\(\vec N\)代表质点受到的理想约束力，那么\(\vec F\)代表该质点受到的主动力，\(\vec r\)代表该质点的位移，则由牛顿第二定律有：

$$\vec F+\vec N=m\ddot{\vec r}\tag{2-1}$$将上式同时乘以虚位移开始消去约束力：$$\vec F\delta\vec r+ \vec N\delta\vec r=m\ddot{\vec r}\delta\vec r\tag{2-2}$$由上文推导的理想约束力的性质，发现左侧第二项事实上就是虚功\(\vec N\delta\vec r=0\)则有如下式子：$$(\vec F-m\ddot{\vec r})\delta\vec r=0 \tag{2-3}$$上式中$latex-m\ddot{\vec r}$称之为惯性力，例如常常被高中物理视作经典错误的“离心力”，式2-3的结论可以推广到n个质点的多质点系统，得到下式也就是达朗贝尔定理：

$$\sum_\limits{i=1}^{i\le n}\left(\vec F_i-m_i\ddot{\vec r_i}\right)\delta\vec {r_i}=0\tag{2-4}$$上式为拉格朗日力学中的第二个基本原理，称之为“动力学普遍方程”，第一基本原理即为相对性原理（事实上这个原理几乎是所有运动力学理论体系中的底层原理，属实称得上是某种公理了），在上式中如果系统处于平衡态也就是所有质点加速度为0的状况下，得到虚功原理如下：$$\sum_\limits{i=1}^{i\le n}\vec F_i\delta\vec {r_i}=0\tag{2-5}$$

在上述推导中使受过经典中国高中教育的同学如鲠在喉的一点就是，这个模型正确但几乎毫无用处，因为其使用的虚位移具有太多运算和实际使用过程中的限制，并且其任意性太大了，导致式2-5几乎无法用于稍微复杂的动力学系统分析，因此可以考虑将虚位移从式2-5中彻底消掉。不同于上式带来的直觉，事实上由于牛顿第二定律的基础分析，可以看到\(\delta\vec{r_i}\)事实在无约束的状况下上可以独立的分离出来也就是整个式子退化为最基础的牛顿第二定律的简单叠加。但是在具有约束的状况下这种分离就毫无依据并且会使得动力学模型的构建出现致命问题。

事实上，去掉虚位移是拉格朗日方程的精髓，归根结底处理的思路是“从另一个角度看待问题”，现在的方程即式2-5的分解和组合方式还是以单个质点的运动为中心，这造成了质点的受力与其运动状态不可分离为单纯的乘积，假设说用”以广义坐标的单个纬度为中心“的方式去重构方程即可以完成虚位移的脱离工作。假设现有系统包括n个质点，那么在三维空间中进行笛卡尔直角坐标系的分解就有3n个坐标去完全的描述整个系统的运动状态。假设系统中含有q个理想约束，那么在广义坐标中，系统的将拥有3n-q个独立维度来描述当前状态。那么设有s个广义坐标量\(q_1,q_2,\cdots,q_s\)则有如下推导方法：

$$\vec{r_i}=\vec{R_i}(q_1,q_2,\cdots,q_n,t)\tag{2-6}$$ $$\delta\vec{r_i}=d\vec{r_i}=\frac{\partial \vec{r_i}}{\partial q_1}dq_1+\frac{\partial \vec{r_i}}{\partial q_2}dq_2+\cdots+\frac{\partial \vec{r_i}}{\partial q_n}dq_n+\frac{\partial \vec{r_i}}{\partial t}dt\tag{2-7}$$ $$\delta\vec{r_i}=\sum_\limits{j=1}^{j\le s}\frac{\partial \vec{r_i}}{\partial q_j}\delta q_j+\frac{\partial \vec{r_i}}{\partial t}\delta t\tag{2-8}$$而事实上根据虚位移的定义，“在无穷小的时间中完成的任意方向无穷小位移”可得\(\delta t=0\)，故上式中有关于时间的量可以消去，将上式代入式2-5可得：

$$\sum_\limits{i=1}^{i\le n} \left[(\vec{F_i}-m_i\ddot {\vec r_i})\bullet\sum_\limits{j=1}^{j\le s}\frac{\partial \vec{r_i}}{\partial q_j}\delta q_j\right]=0\tag{2-9}$$由于虚位移尚未完全从乘积中分离出来，对上式继续做变换将求和次序交换，并考虑到广义积分各项\(\delta q_j\)相互独立，故而消去虚位移如下：

$$\sum_\limits{j=1}^{j\le s}\left[\sum_\limits{i=1}^{i\le n}(\vec{F_j}-m_i\ddot{\vec r_i})\frac{\partial \vec {r_i}}{\partial q_j}\right]\bullet \delta q_j=0\tag{2-10}$$ $$\sum_\limits{i=1}^{i\le n}(\vec{F_j}-m_i\ddot {\vec r_i}) \frac{\partial \vec{r_i}}{\partial q_j}=0\tag{2-11}$$此时就从方程中完全消去了虚位移的影响，这个方程可以理解为，各个质点收到的理想约束（主动力与质点惯性力的矢量和）在广义坐标系中任何一个维度的等效合成作用为0，需要处理的仅仅就剩下了各个质点的位移矢量\(\vec{r_i}\)相关量。为了更好的分解这个方程将其整理成为下式：

$$\sum_\limits{i=1}^{i\le n}\vec{F_i}\frac{\partial \vec{r_i}}{\partial q_j}-\sum_\limits{i=1}^{i\le 0}m_i\ddot {\vec r_i}\frac{\partial \vec{r_i}}{\partial q_j}=0\tag{2-12}$$上式中\(\frac{\partial \vec{r_i}}{\partial q_j}\) 这一项其实就是笛卡尔坐标系对广义坐标系的转换映射，求偏导很容易，因此无需处理，真正需要处理的是加速度\(\ddot{\vec{r_i}}\)这一项。显然如果按照正常的思路先将\(\vec{r_i}\)使用广义坐标表出后再对s项广义坐标求二阶导数将会导致运算非常臃肿，故而使用微分性质d(uv)=vdu+udv对式2-12中的第二项进行变换如下：

$$\sum_\limits{i=1}^{i\le n}m_i\ddot{\vec{r_i}}\frac{\partial \vec{r_i}}{\partial q_j}=\frac{d}{dt}\left(\sum_ \limits{i=1}^{i\le n}m_i\dot{\vec{r_i}}\frac{\partial \vec{r_i}}{\partial q_j}\right)-\sum_\limits{i=1}^{i\le n}m_i \dot{\vec{r_i}}\frac{d}{dt}\frac{\partial \vec{r_i}}{\partial q_j}\tag{2-13}$$此时需要引入著名的拉格朗日关系即如下两个结论：

$$\left\lbrace\begin{array}{c}\frac{\partial \vec{r_i}}{\partial q_j}=\frac{\partial \dot{\vec{r_i}}}{\partial \dot{q_j}}\\\frac {d}{dt}\left(\frac{\partial\vec{r_i}}{\partial q_j}\right)=\frac{\partial}{\partial q_j}\left(\frac {d\vec{r_i}}{dt}\right)\end{array}\right.\tag{2-14}$$接下来对这两个拉格朗日关系进行简短的证明如下：

$$\dot{\vec{r_i}}=\sum_\limits{k=1}^{k\le s}\frac{\partial\vec{r_i}}{\partial q_k}\dot{q_k}\frac{\partial \vec r_i}{\partial t}\tag{2-15}$$

$$\frac{\partial \dot{\vec r_i}}{\partial \dot{q_j}}=\frac{\partial}{\partial \dot{q_j}}\left(\sum_\limits{k=1} ^{k\le s}\frac{\partial \dot{\vec r_i}}{\partial q_k}\dot{q_k}+\frac{\partial \vec r_i}{\partial t}\right)\tag{2-16}$$在式2-16中t和\(q_k,(k\neq j)\)相关的项都与\(\dot q_j\)无关可以消去，得出如下式子完成拉格朗日关系中第一部分的证明：$$\frac{\partial \dot{\vec r_i}}{\partial \dot{q_j}}=\frac{\partial}{\partial \dot q_j}\left(\frac{\partial \vec{r_i}}{\partial q_j}\dot q_j\right)=\frac{\partial\vec {r_i}}{\partial q_j}\tag{2-17}$$

$$\frac{\partial \dot{\vec r_i}}{\partial q_j}=\frac{\partial}{\partial q_j}\left(\sum_\limits{k=1} ^{k\le s}\frac{\partial \dot{\vec r_i}}{\partial q_k}\dot{q_k}+\frac{\partial \vec r_i}{\partial t}\right)=\sum_\limits {k=1}^{k\le s}\frac{\partial^2 \vec{r_i}}{\partial q_k\partial q_j}+\frac{\partial^2 \vec{r_i}}{\partial p_j \partial t}\tag{2-18}$$ $$\frac{\partial \dot{\vec r_i}}{\partial q_j}=\sum_\limits{k=1}^{k\le s}\frac{\partial}{\partial q_k}\left(\frac{\partial \vec r_i}{\partial q_j}\right)\dot{q_k}+\frac{\partial}{\partial t}\left(\frac{ \partial \vec{r_i}}{\partial q_j}\right)=\frac{d}{dt}\left(\frac{\partial \vec r_i}{\partial q_j}\right)\tag{2-19} $$ $$\frac{\partial}{\partial q_j}\left(\frac{d\vec r_i}{dt}\right)=\frac{\partial \dot{\vec r_i}}{\partial q_j}=\frac {d}{dt}\left(\frac{\partial \vec r_i}{\partial q_j}\right)\tag{2-20}$$由式2-15、2-18、2-19可以证明得出拉格朗日关系的第二个式子如式2-20。代入拉格朗日关系的两个式子到式2-13中，可以得到如下结果：

$$\sum_\limits{i=1}^{i\le n}m_i\ddot{\vec{r_i}}\frac{\partial \vec{r_i}}{\partial q_j}=\frac{d }{dt}\left(\sum_\limits{i=1}^{i\le n}m_i\dot{\vec r_i}\frac{\partial \dot{\vec r_i}}{\partial \dot{q_j}}\right)-\sum_\limits{i=1}^{i\le n}m_i\dot{\vec r_i}\frac{\partial}{\partial q_j}\left( \frac{d\vec r_i}{dt}\right)\tag{2-21}$$对2-21式中的积分符号与求和符号顺序进行调整可得到如下结果：

$$\sum_\limits{i=1}^{i\le n}m_i\ddot{\vec{r_i}}\frac{\partial \vec{r_i}}{\partial q_j}=\frac{d }{dt}\frac{\partial}{\partial \dot q_j}\left(\sum_\limits{i=1}^{i\le n}\frac 12 m_i\dot{\vec {r_i }}^2\right)-\frac{\partial}{\partial q_j}\left(\sum_\limits{i=1}^{i\le n}\frac 12 m_i\dot{\vec{r _i }}^2\right)\tag{2-22}$$可以看到经过上式中的一系列变换后，出现了一个特殊项则可以设第i个质点的动能为\(T_i=\frac 12 m_i\dot{\vec {r_i }}^2\)那么可以得到式2-22的简便表示方法如下：

$$\sum_\limits{i=1}^{i\le n}m_i\ddot{\vec r_i}\frac{\partial\vec r_i}{\partial \dot q_j}= \frac{ d}{dt}\frac{\partial T}{\partial\dot q_j}-\frac{\partial T}{\partial q_j}\tag{2-23}$$将式2-13中的第一项表示为广义力\(Q_j\)代表着各个质点上的主动力投射在广义坐标方向\(q_j\)方向上的矢量和，也就是整个系统中质点向该方向的受力，再代入式2-23至2-13中，得到简化表达方式：

$$Q_j-\frac{d}{dt}\frac{\partial T}{\partial \dot q_j}+\frac{\partial T}{\partial q_j}=0\tag{2-24}$$$$\frac{d}{dt}\frac{\partial T}{\partial \dot q_j}-\frac{\partial T}{\partial q_j}=Q_j,\,(j=1,2,\cdots,s)\tag{2-25}$$这一组方程即为拉格朗日方程，单个方程用于描述在广义坐标某一方向上的状态，T表示体系动能，\(q_j\)为广义坐标，\(Q_j\) 为广义力，\(\dot q_j\)为广义坐标速度，还可以定义广义动量为\(P_j=\frac{ \partial T}{\partial \dot q_j}\)，细心观察拉格朗日方程事实上是牛顿第二定律的另一种表达方式，也算是逻辑推导上的自洽。

3.保守力与约束完整性问题

在上文的推导中求出了拉格朗日方程，拉格朗日方程存在一种较为特殊的情况，也就是力学系统中所受到的所有主动力全部都是保守力，而保守力决定了力学系统肯定存在各种各样的势能U，并且这个势能U显然只和各个质点的位置矢量\(\vec r_i\)相关，于是有\(U=U(\vec r_1,\vec r_2,\cdots,\vec r_n)\)显然使用U表示的主动力和广义力如下：$$\vec{F_i}=-\frac{\partial U}{\partial\vec{r_i}}\tag{3-1}$$

$$Q_j=\sum_\limits{i=1}^{i\le n}-\frac{\partial U}{\partial\vec{r_i}}\frac{\partial\dot{\vec r_i}}{\partial q_j}=- \frac{\partial U}{\partial q_j}\tag{3-2}$$也就是说保守系统中的广义力可以视为系统势能在相应广义坐标上的偏导数相反数，符合势能的定义，代入式2-25可得：

$$\frac{d}{dt}\frac{\partial T}{\partial\dot q_j}-\frac{\partial T}{\partial q_j}=-\frac{\partial U}{\partial q_j} \tag{3-3}$$ $$\frac{d}{dt}\frac{\partial(T-U)}{\partial\dot q_j}-\frac{\partial(T-U)}{\partial q_j}=0\tag{3-4}$$ 上式中第一项的原因是系统势能实际上和广义速度无关，当然其对广义速度的导数也就是0，写成这个形式主要是为了引出拉格朗日函数\(L=T-U\)，用这个函数可以得到保守体系下完整约束系统的拉格朗日方程如下所示：$$\frac{d}{dt}\frac{\partial L}{\partial\dot q_j}-\frac{\partial L}{\partial q_j}=0\tag{3-5}$$

在推导保守体系下系统拉格朗日方程中提到了一个概念“完整约束系统”，这就需要定义什么系统的约束是完整的而什么又是不完整的。完整约束也就是几何约束，这种约束表现在各个质点的几何关系上，通常表示为\(f(x,y,z)=0\)仅仅与系统质点的位置有关。较为特殊的就是涉及到滚动转动的运动系统，例如一个刚性球在地面上纯滚动，对于其速度有\(\dot x-R\dot\theta=0\)，显然我们发现这个方程是可积的，通过积分可以得到\(x-R\theta=0\)就转换为了几何约束，这种方式叫做微分约束，可以通过积分变换为几何约束也就是完整约束。那么不完整约束的定义也就呼之欲出了：某种不能通过积分变换为几何约束的微分约束，他就对应着不完整系统。

如果对于方程组较为敏感的同学，应当已经发现了致命问题，s个广义坐标中却出现了u个非完整约束，这就导致了原先的广义坐标中只有s-u个是独立的，其余都可以通过其他分量来表出。事实上只要故技重施将其中u个广义坐标前的乘数调整为0即可消去这个量得出仅仅与独立的s-u个坐标对应的方程组。

PS: 可供参考学习的博文和链接

知乎：从零分析力学（拉格朗日力学篇）——作者：你的小睿子
百度文库：动力学普遍方程及拉格朗日方程——上传：孤山望世界
CSDN：动力学建模-拉格朗日建模——作者在路上@Amos